7.8 归并排序

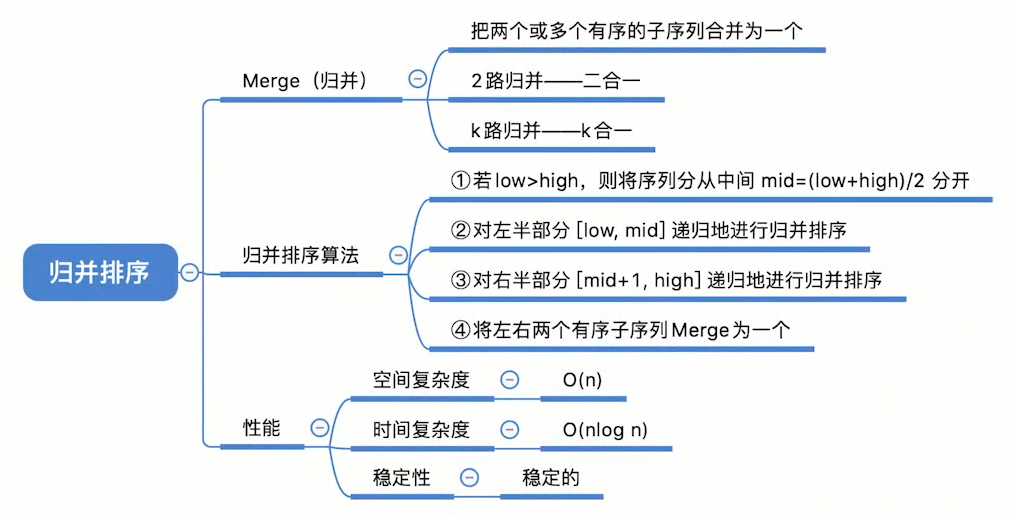
归并排序是建立在归并操作上的一种有效的排序算法。该算法是采用分治法（Divide and Conquer）的一个非常典型的应用。将已有序的子序列合并，得到完全有序的序列；即先使每个子序列有序，再使子序列段间有序。

归并：把两个或多个已经有序的序列合并成一个。

m路归并：将m个有序的序列合并成一个，每选出一个元素需要对比关键字m-1次。

2路归并：

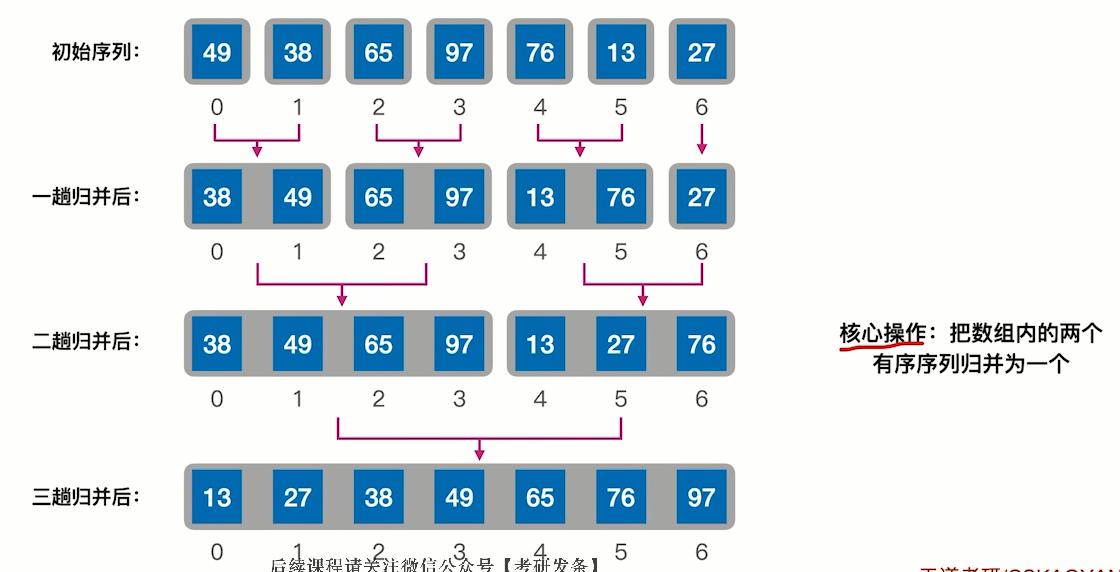
7.8.1 算法思想：

• 把长度为n的输入序列分成两个长度为n/2的子序列；
• 对这两个子序列分别采用归并排序；
• 将两个排序好的子序列合并成一个最终的排序序列。

img

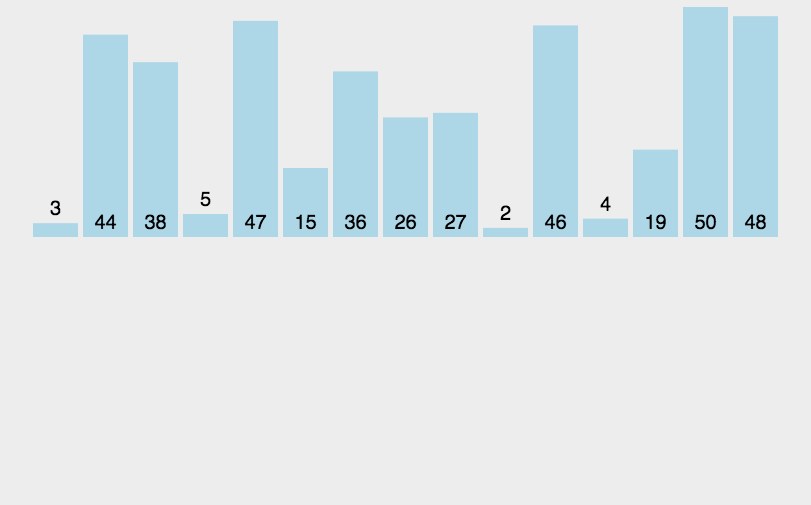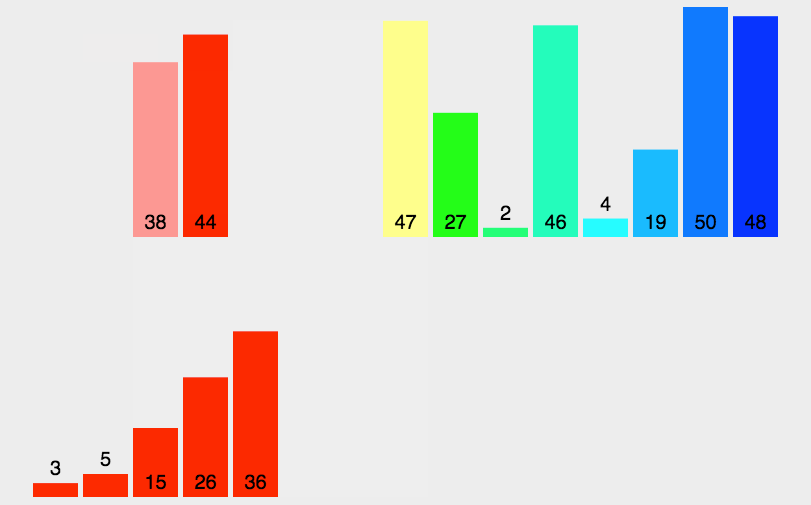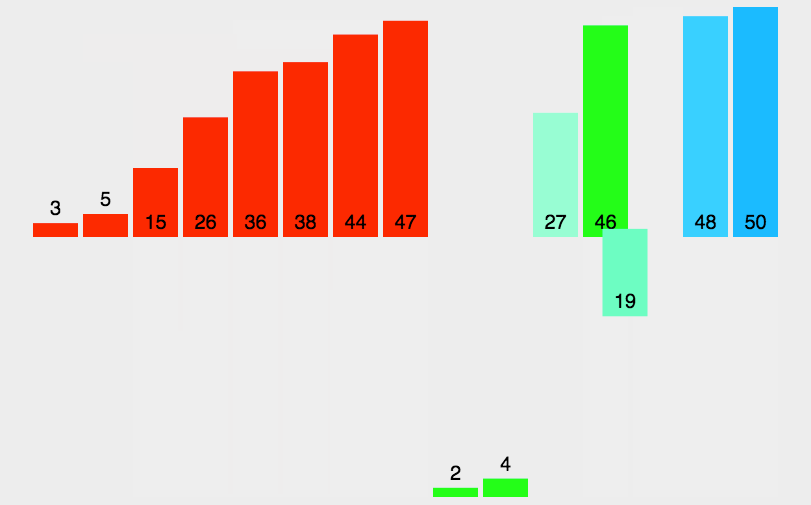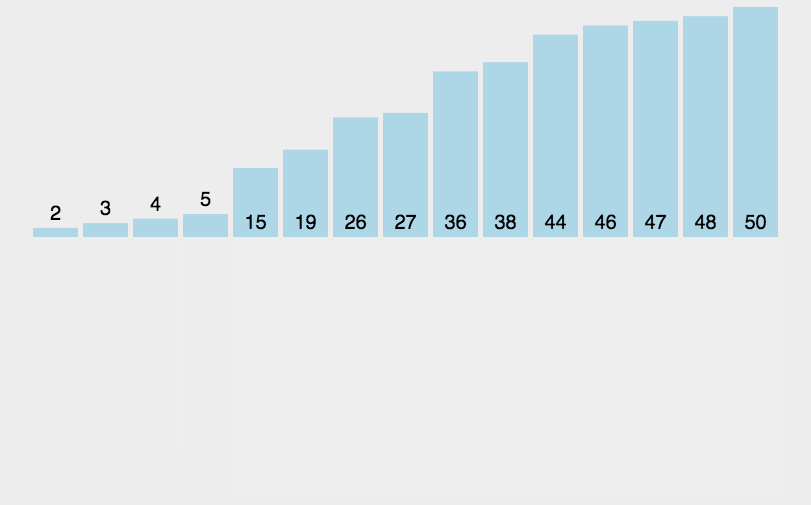
7.8.2 代码实现：

int *B = (int *)malloc(n*sizeof(int)); //辅助数组B
//将两个有序数组归并（A[low...mid]和A[mid+1...high]各自有序，将两个部分归并）
void Merge(int A[],int low,int mid,int high){
    int i,j,k;
    for(k=low; k<=high; k++){
        B[k] = A[k];
    }
    for(i=low,j=mid+1,k=i; i<=mid&&j<=high; k++){
        if(B[i]<=B[j]) A[k] = B[i++];     //将较小的复制到A中，先赋值，再将指针后移。
        else A[k] = B[j++];
    }
    while(j<=mid) A[k++] = B[i++];    //先赋值，再将指针后移。
    while(j<=high) A[k++] = B[j++];    //先赋值，再将指针后移。
}
//归并排序
void MergeSort(int A[],int low,int high){
    if(low<high){
        int mid = (low+high)/2;   //从中间划分
        MergeSort(A,low,mid);     //对左半部分归并排序
        MergeSort(A,mid+1,high);  //对右半部分归并排序
        Merge(A,low,mid,high);    //归并
    }
}

7.8.3算法效率分析

空间复杂度=$O(n)$，因为需要的辅助数组B

时间复杂度： n个元素进行二路归并，需进行$\lceil log_2n \rceil$趟 每趟归并的时间复杂度=$O(n)$

时间复杂度=$O(nlog_2n)$

算法稳定性：稳定

顺序表和链表都可以。