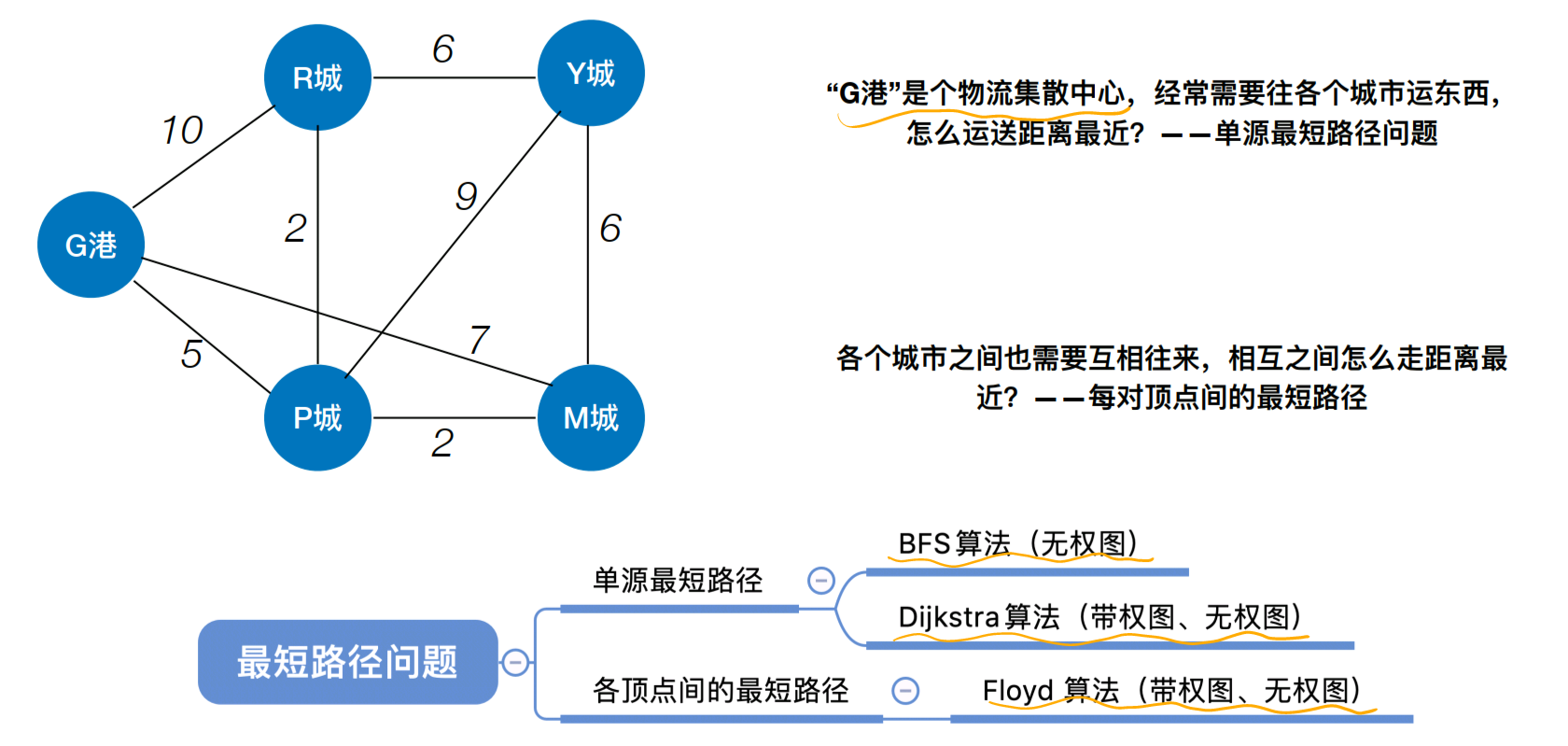
5.6 最短路径

1638172106501

1638178148141

5.6.1 BFS算法（无权图）

由广度优先算法求最短路径：

//图的广度优先搜索（用图的邻接矩阵、领接表都可以，只是FirstNeighbor和NextNeighbor函数实现不一样）
bool visited[MAX_VERTEX_NUM];     //访问标记数组
void BFSTraverse(Graph G){        //对图G进行广度优先搜索
    for(v=0; v<G.vexnum; ++v){
        visited[v] = false;       //初始化访问标记数组
    }
    InitQueue(Q);                 //初始化辅助队列Q
    for(v=0; v<G.vexnum; ++v){
        if(!visited[v]){          //对每个连通分量调用一次BFS
            BFS(G,v);             //vi没访问过，从vi开始BFS
        }
    }
}
void BFS(Graph G, int v){
	visit(v);             //访问初始顶点v
    visited[v] = true;    //对v做已访问标记
    EnQueue(Q, v);        //顶点v入队
    while(!isEmpty(Q)){   //队列不空则循环
        DeQueue(Q, v);    //顶点v出队
        for(w=FirstNeighbor(G,v); w>=0; w=NextNeighbor(G,v,w)){//检测v所有的邻接顶点
            if(!visited[w]){          //w为v尚未访问的邻接顶点
				visit(w);             //访问顶点w
    			visited[w] = true;    //对w做已访问标记
                EnQueue(Q, w);        //顶点w入队
            }
        }
    }
}

实现方式： 用两个数组： ①d数组：记录各点的路径长度。 ②path数组：记录各点的前驱。

时间复杂度：

邻接矩阵=$O(|V|^2)$，邻接表=$O(|V|+|E|)$

//用BFS求顶点U到其它顶点的最短路径（只改了visit函数调用的两行）
#define INFINITY 4294967295       //宏定义常量“无穷”，4294967295为最大的int值
bool visited[MAX_VERTEX_NUM];     //访问标记数组
void BFS(Graph G, int v){
	//d[i]表示从u到i结点的最短路径
    for(i=0; i<G.vexnum; ++i){
        d[i] = INFINITY;  //初始化路径长度
        path[i] = -1;     //最短路径从哪个顶点过来
    }
    d[u] = 0;             //从u开始
    visited[v] = true;    //对v做已访问标记
    EnQueue(Q, v);        //顶点v入队
    while(!isEmpty(Q)){   //队列不空则循环
        DeQueue(Q, v);    //顶点v出队
        for(w=FirstNeighbor(G,v); w>=0; w=NextNeighbor(G,v,w)){//检测v所有的邻接顶点
            if(!visited[w]){          //w为v尚未访问的邻接顶点
				d[w] = d[u] + 1;      //路径长度加1
                path[w] = u;          //最短路径应从u到w
    			visited[w] = true;    //对w做已访问标记
                EnQueue(Q, w);        //顶点w入队
            }
        }
    }
}

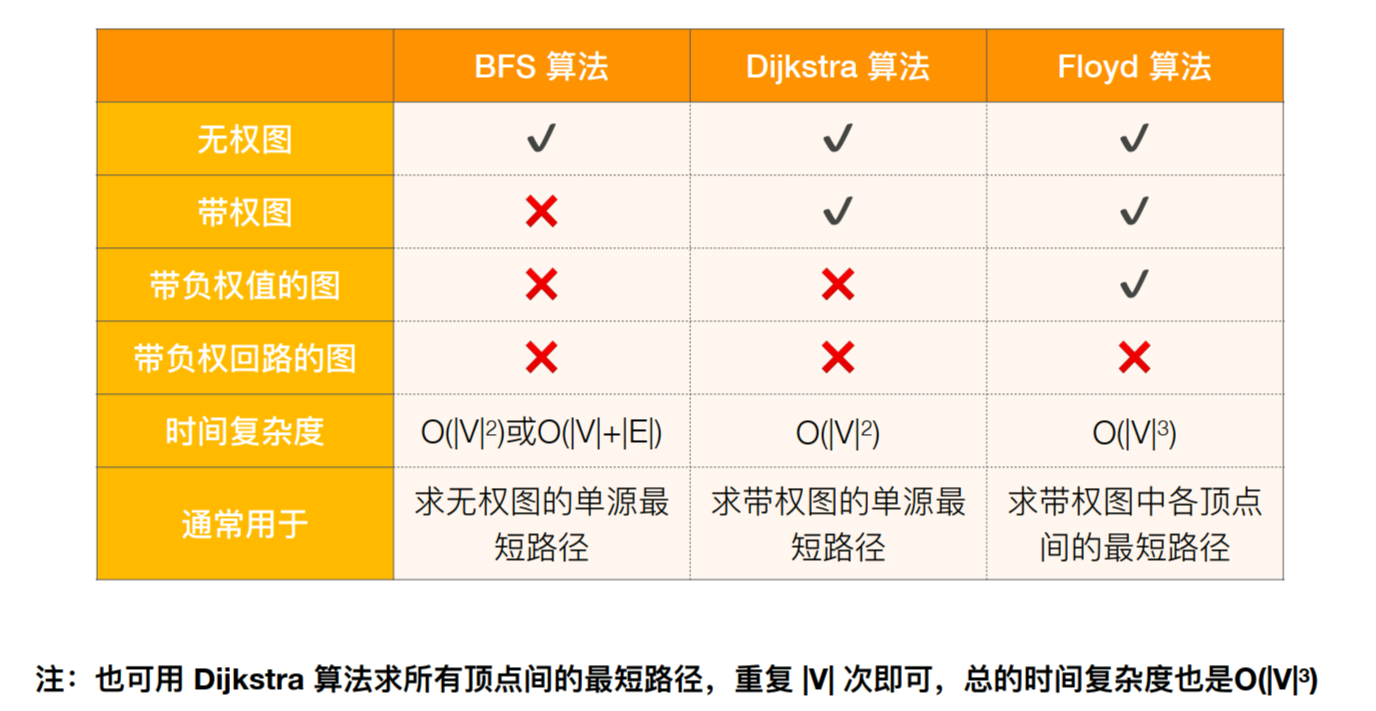
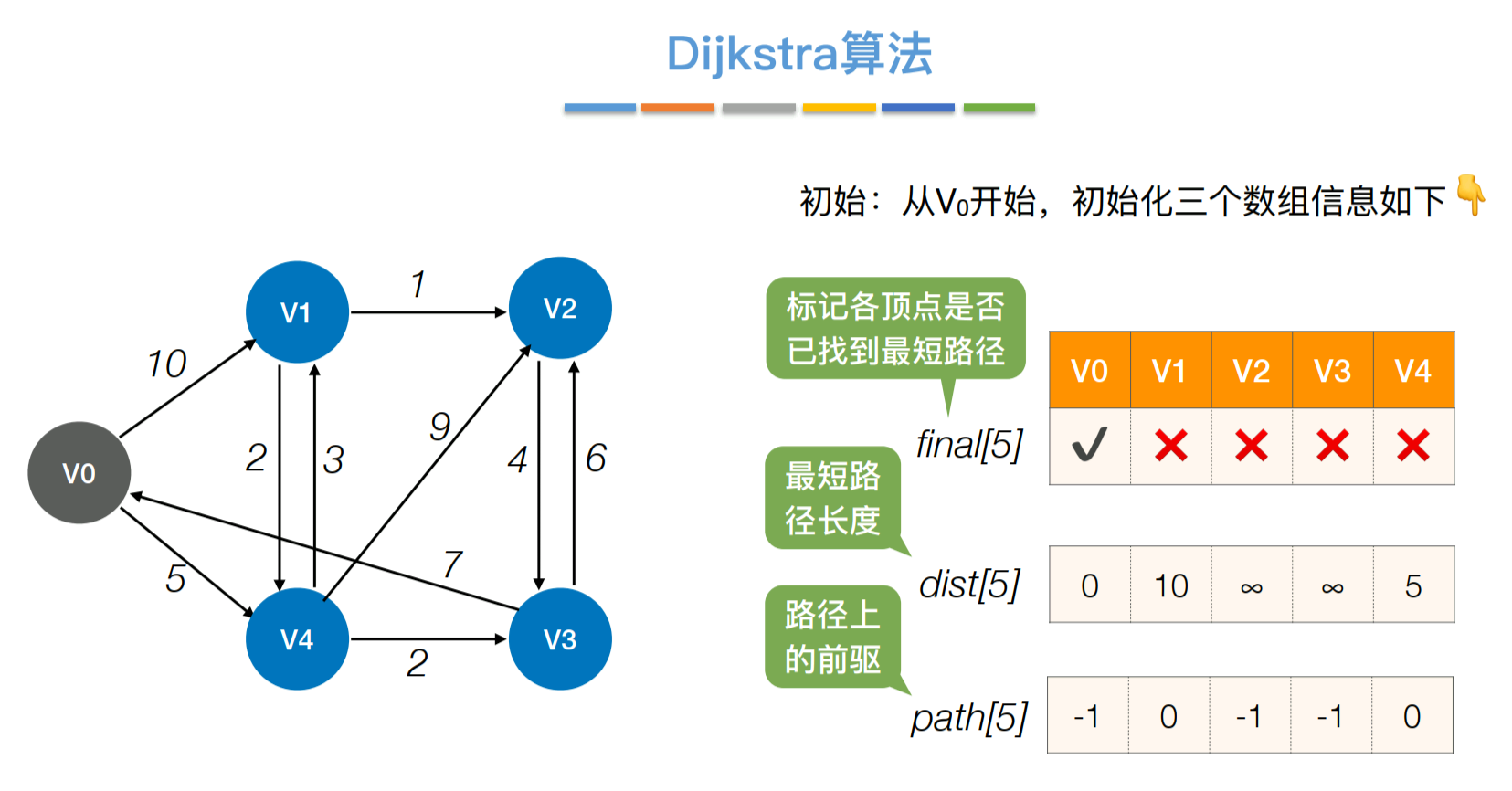
5.6.2 Dijkstra算法（迪杰斯特拉算法）（带权图、无权图）

BFS算法的局限性：不适用带权图

实现方式： 用两个数组：

• ①final数组：记录各顶点是否已找到最短路径。
• ②dist数组：记录各点的最短路径长度。
• ③path数组：记录各点路径上的前驱。

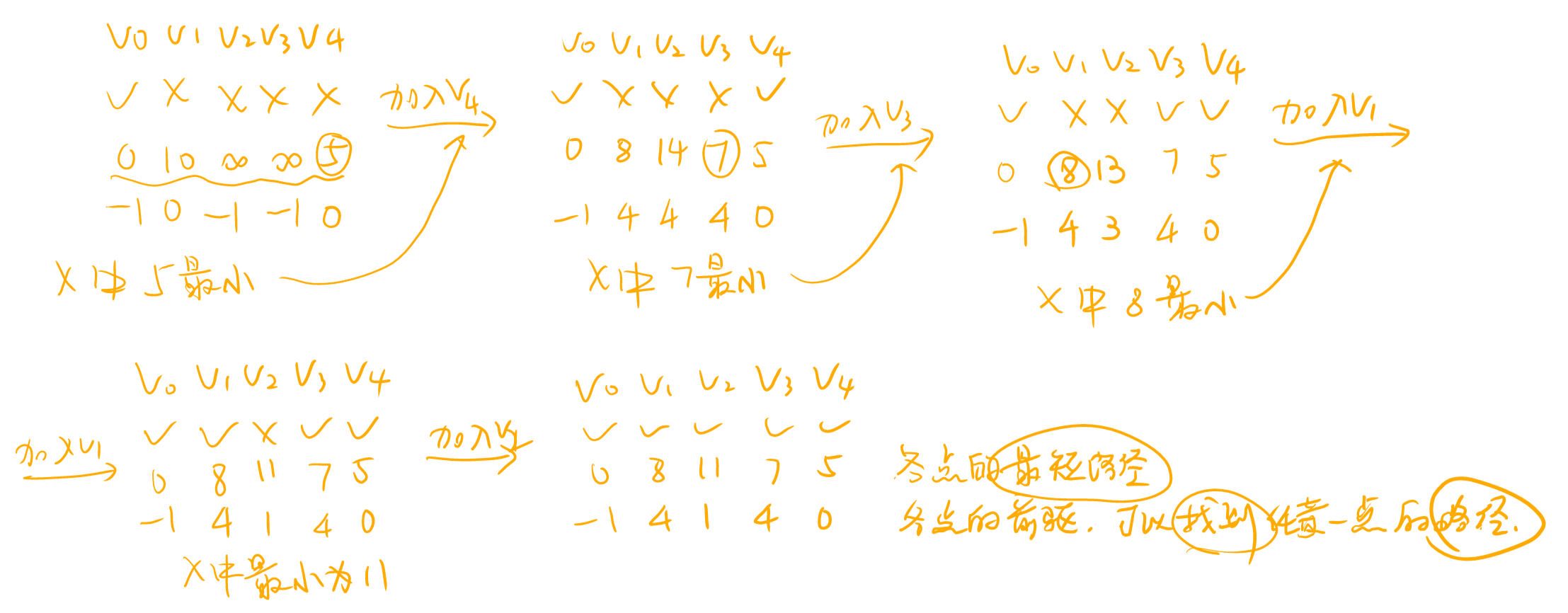
每轮遍历final数组，第一遍找到dist最低的顶点，然后加入；第二遍循环遍历更新各点的dist值和path值。 则时间复杂度=$O(|V|^2)$

Dijkstra算法的局限性：不适用负权值带权图。

1638175026752

1638175026747

5.6.3 Floyd算法（弗洛伊德算法）（带权图、无权图）

实现方式： 用两个二维数组：

• ①A数组：记录各顶点之间目前的最短路径长度
• ②path数组：记录两点之间的第一个中转点。

以某一点为中转点遍历二维数组，更新两个数组，将所有点作为中转点都遍历一遍，形成三重循环 则时间复杂度=$O(|V|^3)$，空间复杂度=$O(|V|^2)$。

Floyd算法的局限性：不适用负权值带权图。

//省略初始化A和path数组
//Floyd算法的核心
for(int k=0; k<n; k++){          //考虑以Vk作为中转点
    for(int i=0; i<n; i++){      //遍历整个矩阵，i为行号，j为列号
    	for(int j=0; ij<n; j++){
        	if(A[i][j] > A[i][k] + A[k][j]){    //以Vk作为中转点的路径更短
                A[i][j] = A[i][k] + A[k][j];    //更新最短路径长度
                path[i][j] = k;                 //中转点
            }
    	} 
    }
}