5.1 图

5.1.1 图的定义

图G由顶点集V和边集E组成，记$G=(V，E)$。

$|V|$表示图G中顶点的个数，也称图G的阶。

$|E|$表示图G中边的条数。

注：线性表可以是空表，树可以是空树，但图不可以为空，即V一定是非空集

5.1.2 图的分类

①有向图和无向图。

1637762644688

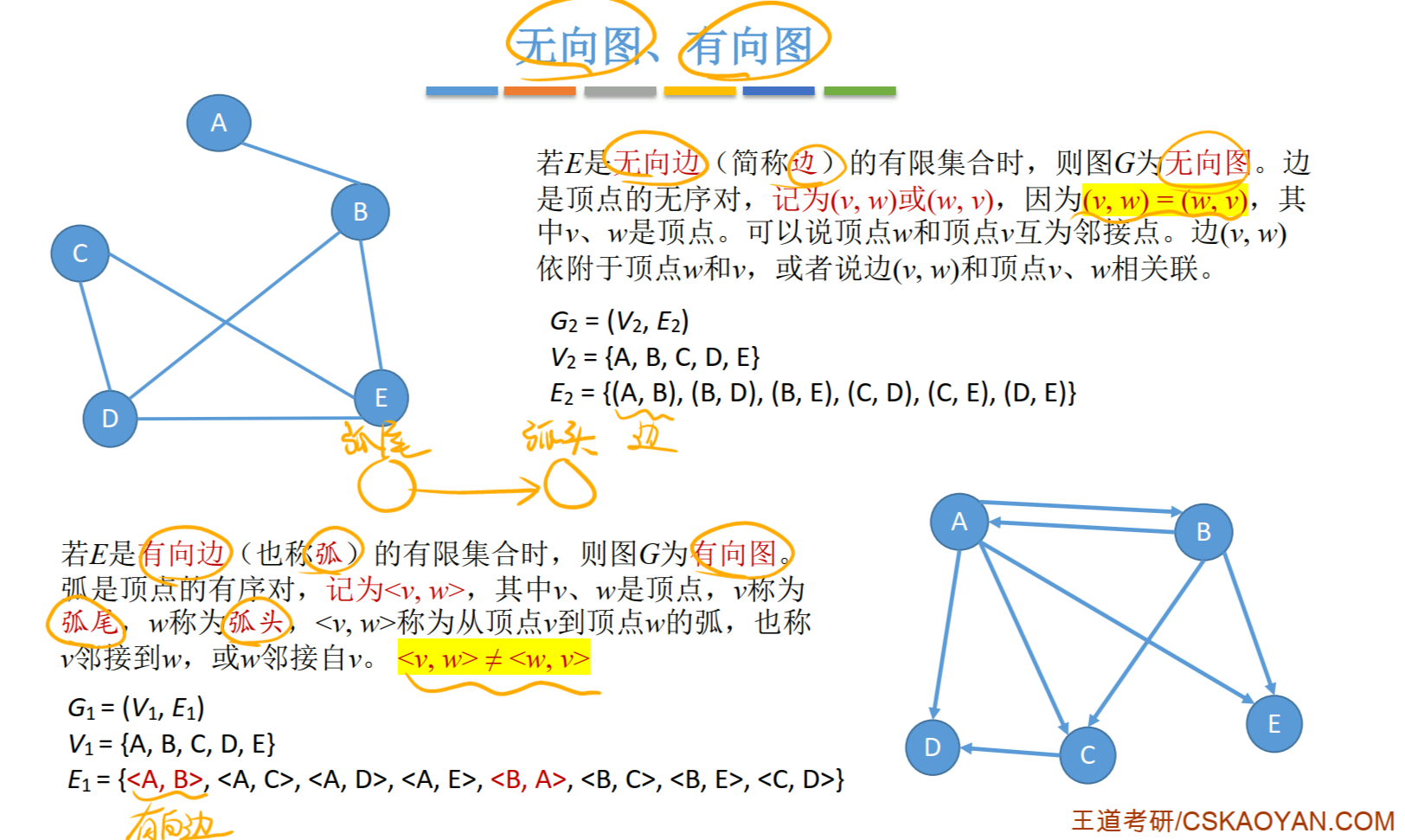
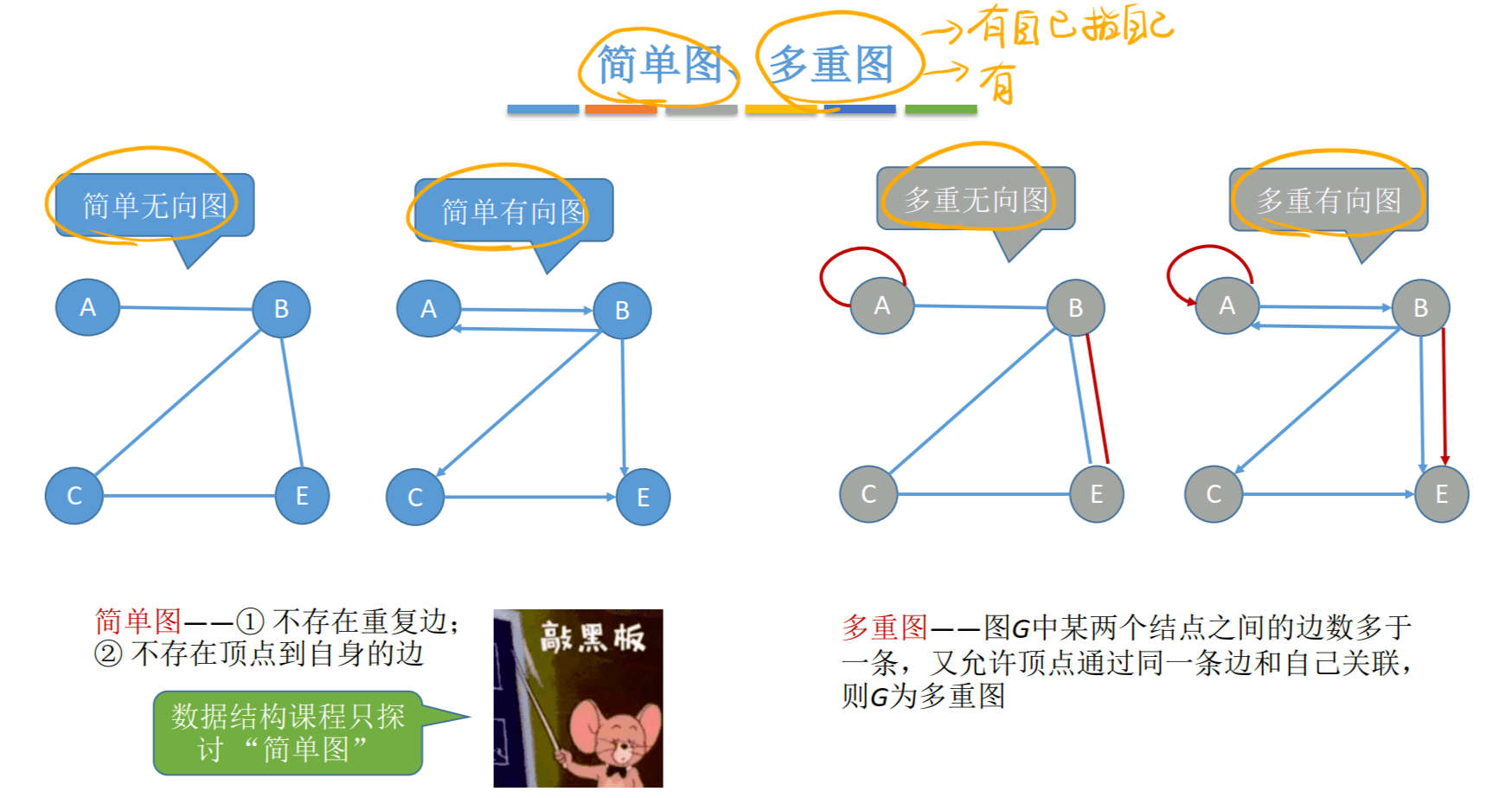
②简单图和多重图

1637762901031

5.1.3 顶点的度，入度、出度

无向图： 顶点的度=连该顶点的边的条数 无入度出度概念

有向图： 入度=指向该点的边的条数 出度=从该点指向其它点的边的条数 顶点的度=连该顶点的边的条数=入度出度之和

5.1.4 顶点与顶点之间的关系

1637763340772

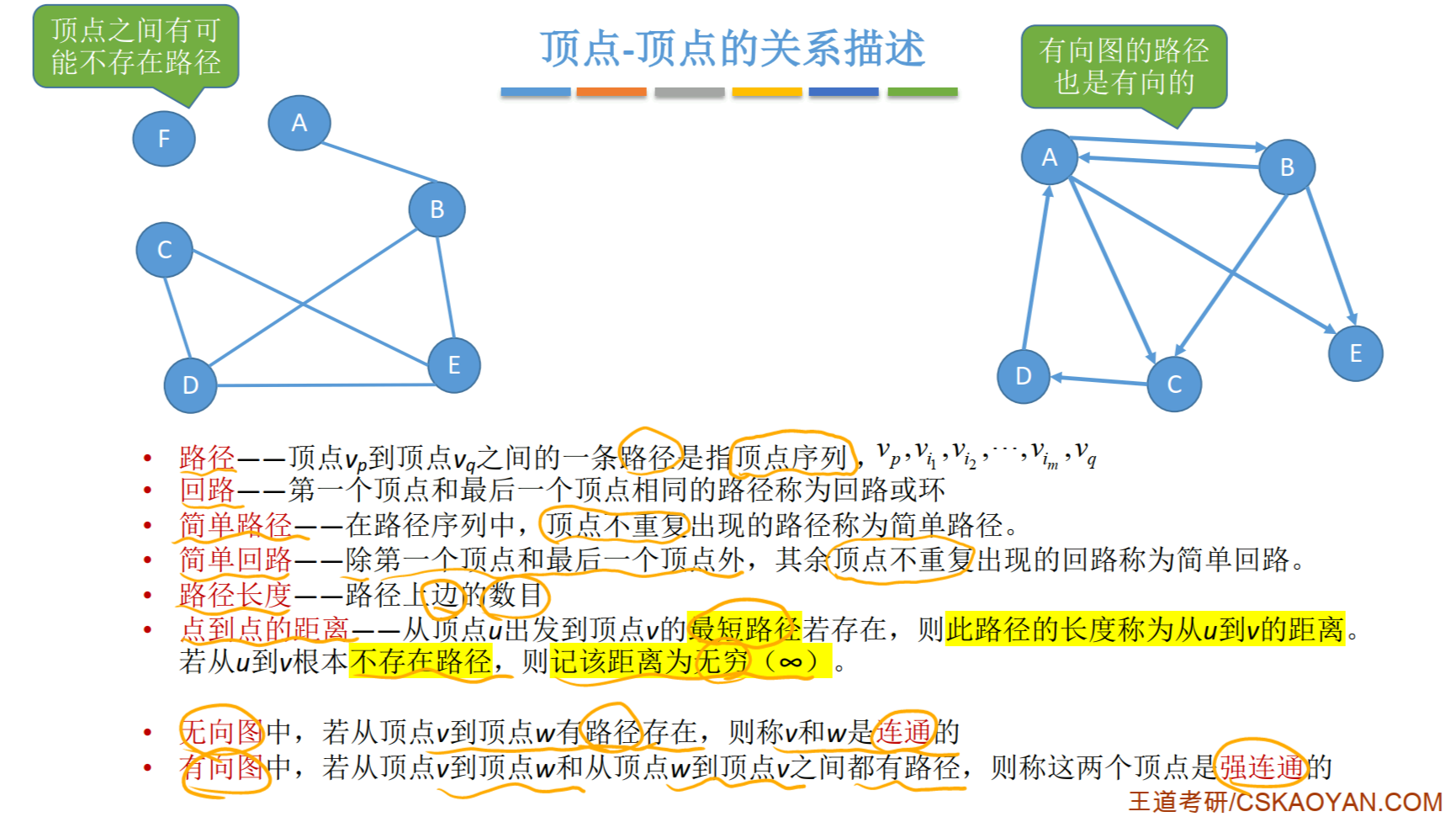
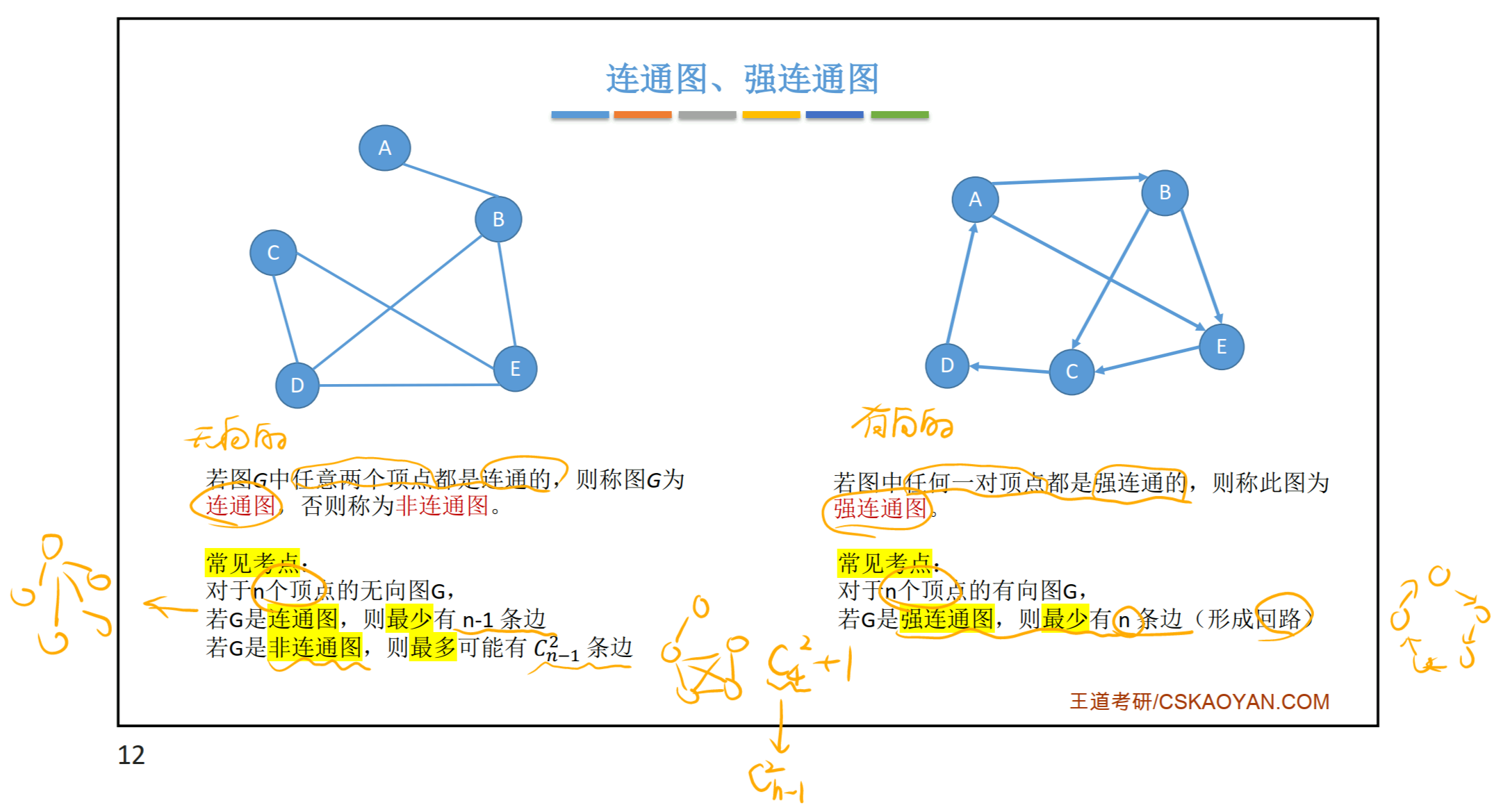
5.1.5 连通图、强连通图

1637763511883

5.1.6 子图、生成子图

子图：点集是子集，边集是子集 生成子图：点集不变，边集是子集。

5.1.7 连通分量、强连通分量

连通分量：无向图的极大连通子图 强连通分量：有向图的极大连通子图

5.1.8 生成树、生成森林

连通图可以生成树 非连通图可以生成森林

5.1.9 特殊的图

①无向完全图、有向完全图

• 无向完全图：无向图中任意两个顶点之间都存在边
• 有向完全图：有向图中任意两个顶点之间都存在相反的两条弧

②稀疏图、稠密图

• 稀疏图：边很少的图
• 稠密图：边很多的图

③树、有向树

• 树：不存在回路、且连通的无向图
• 有向树：一个顶点的入度为0，其余顶点的入度为1 的有向图