4.4 树的存储结构

4.4.1 存储结构

顺序存储和链式存储

方法： 双亲表示法（顺序存储） 孩子表示法（顺序+链式存储） 孩子兄弟表示法（链式存储）

4.4.2 双亲表示法（顺序存储）

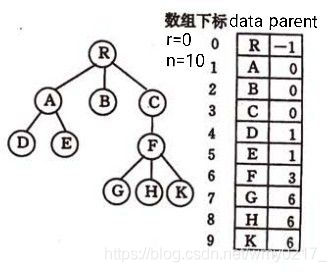
双亲表示法：顺序存储结点数据，结点中保存父结点在数组中的下标

优点：找父节点方便。 缺点：找孩子不方便。

注：双亲表示法与二叉树的顺序存储不一样，双亲表示法也可表示二叉树

类型描述

结点包括数据和父亲下标， 树包括结点数组和结点个数

#define MAX_TREE_SIZE 100         //树中最多结点数
typedef struct{                   //树的结点定义
    ElemType data;                //数据元素
    int parent;                   //双亲位置域
}PTNode;
typedef struct{                   //树的类型定义
    PTNode nodes[MAX_TREE_SIZE];  //双亲表示
    int n;                        //结点数
}PTree;

增加一个结点

新增元素，无需按逻辑次序存储，可以放到删除结点留下的存储空间里

删除一个结点

方案一：数据取出，双亲指针改为-1

方案二：用存储空间中最后一个存的结点把要删的结点覆盖

查找一个结点

找父结点方便、找孩子不方便。

空数据导致遍历慢。

4.4.2 孩子表示法（顺序+链式存储）

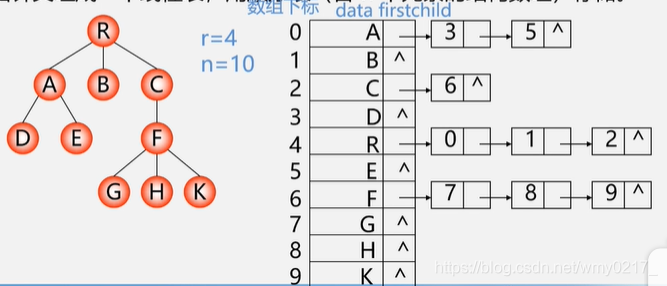
孩子表示法：顺序存储结点数据，结点中保存孩子链表头指针（链式存储）

优点：找孩子方便。 缺点：找父节点不方便。

类型描述

孩子结点包括孩子下标和下一个孩子指针， 数组包括数据和孩子结点， 树包括数组和数组元素（结点）个数及根的下标

#define MAX_TREE_SIZE 100         //树中最多结点数
struct CTNode{
    int child;                    //孩子结点在数组中的位置
	struct CTNode *next;          //下一个孩子
};
typedef struct{
    ElemType data;
	struct CTNode* firstchild;    //第一个孩子
}CTBox;
typedef struct{
    CTBox nodes[MAX_TREE_SIZE];
	int n, r;                     //结点数和根的位置
}CTree;

增加一个结点

新增元素，父结点后新增一个孩子结点，数组中加一个数组元素

删除一个结点

父结点后的链表中将此结点删除

数组中： ①若此结点后无链表，则直接删除 ②若此结点后有链表，再处理子树

查找一个结点

按图一行一行遍历

找孩子结点方便，找父结点不方便

4.4.3 孩子兄弟表示法（顺序+链式存储）

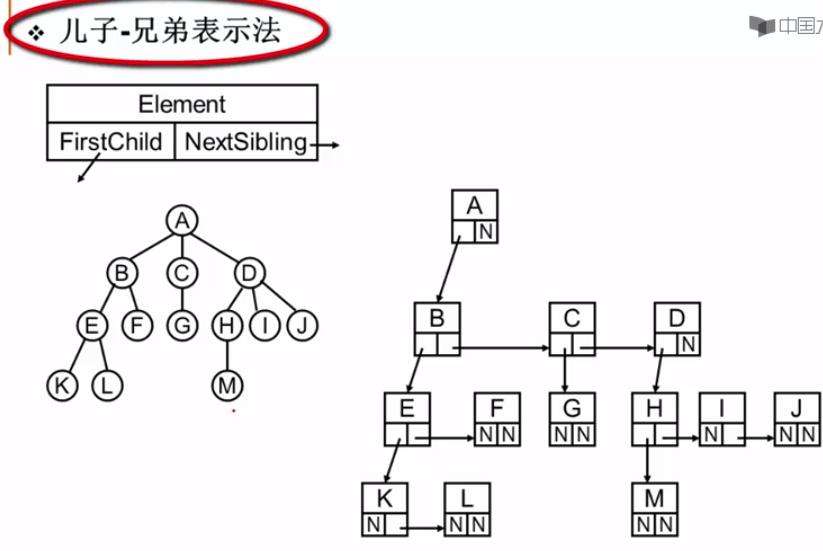
孩子兄弟表示法：用二叉链表存储树——两个指针：第一个孩子和右兄弟

用此方法存储的树，形态上和二叉树类似

类型描述

由二叉树的链式存储（二叉链表）改变而来

typedef struct CSNode{
	Elemtype data;                   //数据域
	struct CSTNode *firstchild, *nextsibling; //第一个孩子和右兄弟指针
}CSTNode, *CSTree;

应用：树和二叉树的转换

1637759667705

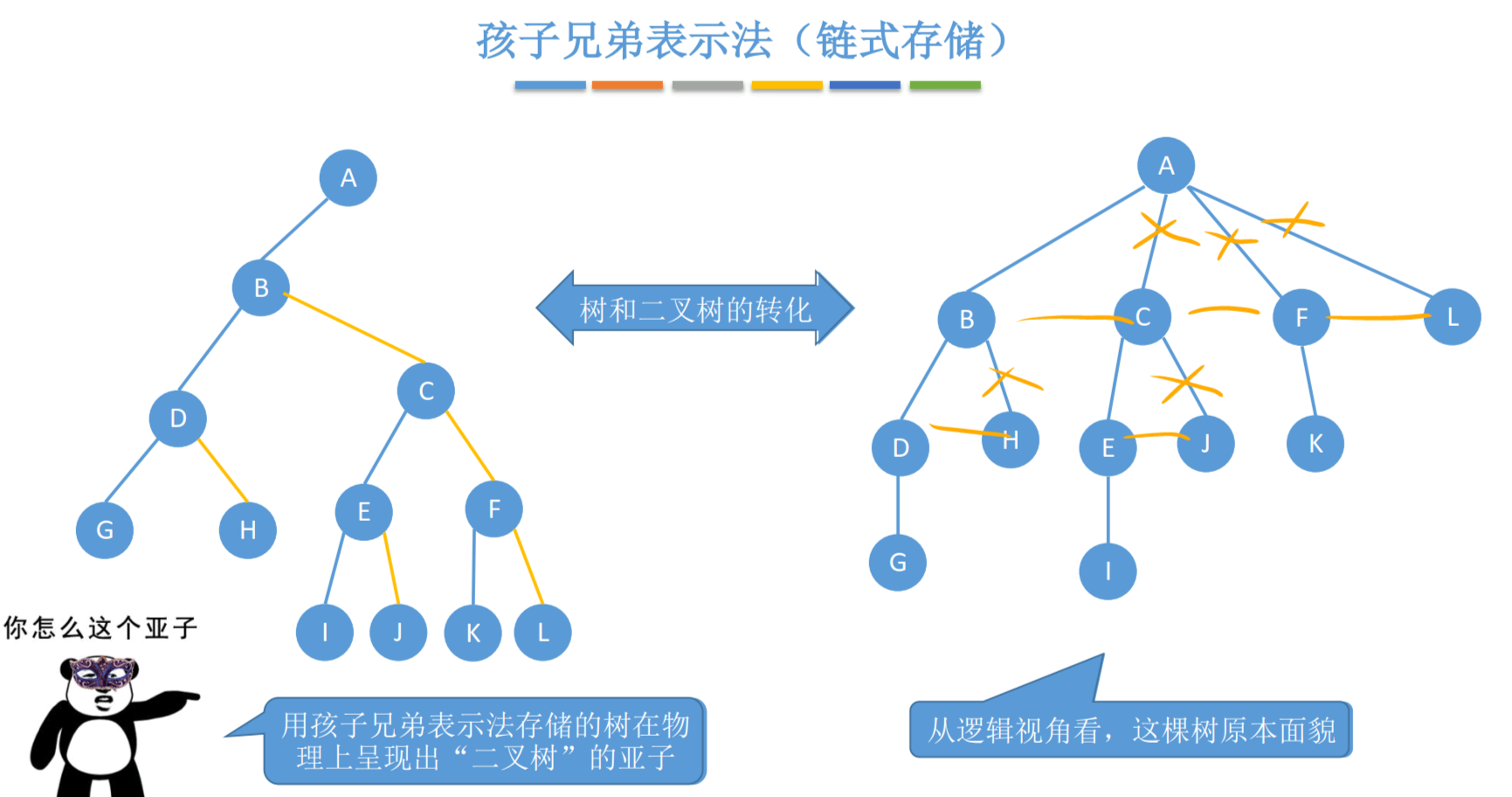
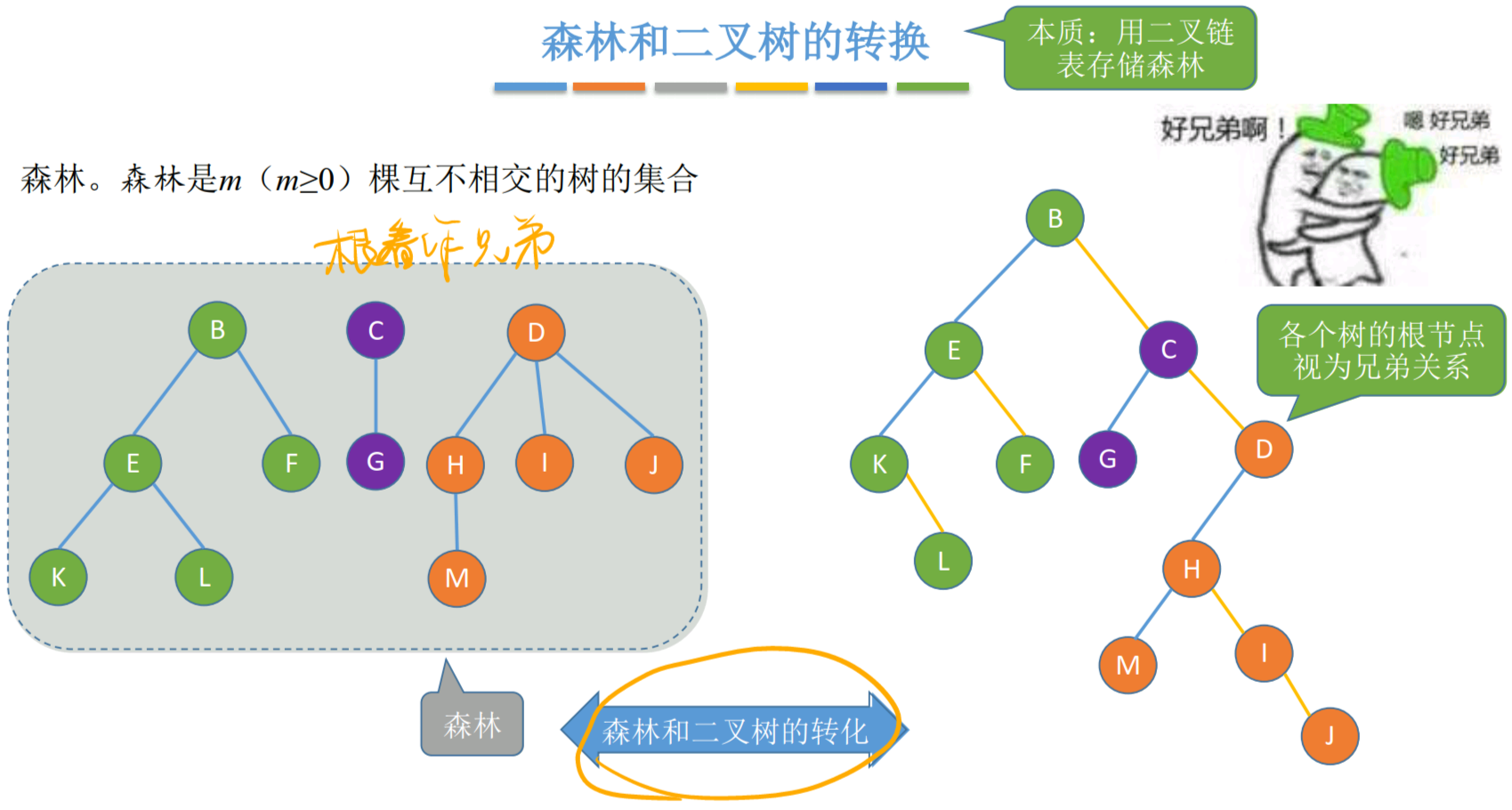
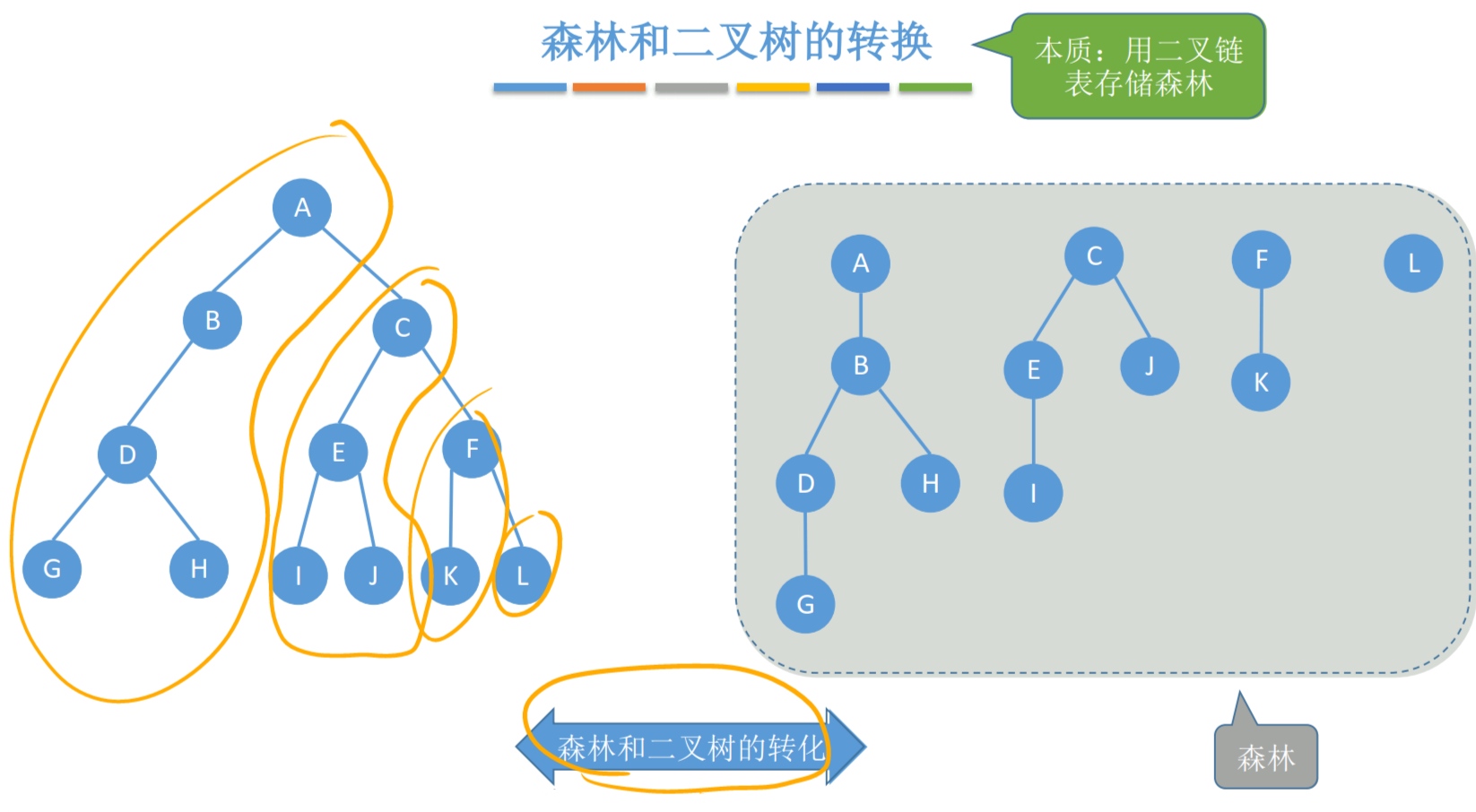
4.4.4 森林和二叉树的转换

本质：用二叉链表存储森林

将森林的根结点连起来，视为兄弟关系

1637759667694

1637759667683