4.2 二叉树
4.2 二叉树
4.2.1 二叉树的定义:
二叉树是n(n≥0)个结点的有限集合 ①或者为空二叉树,即n=0。 ②或者由一个根结点和两个互不相交的被称为根的左子树和右子树组成。左子树和右子树又分别是一棵二叉树 特点:①每个结点至多只有两棵子树 ②左右子树不能颠倒(二叉树是有序树)
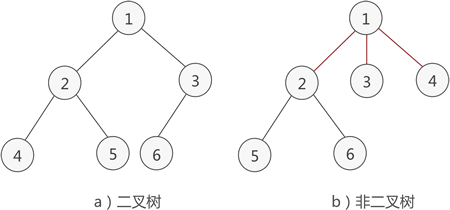
4.2.2 二叉树的五种状态
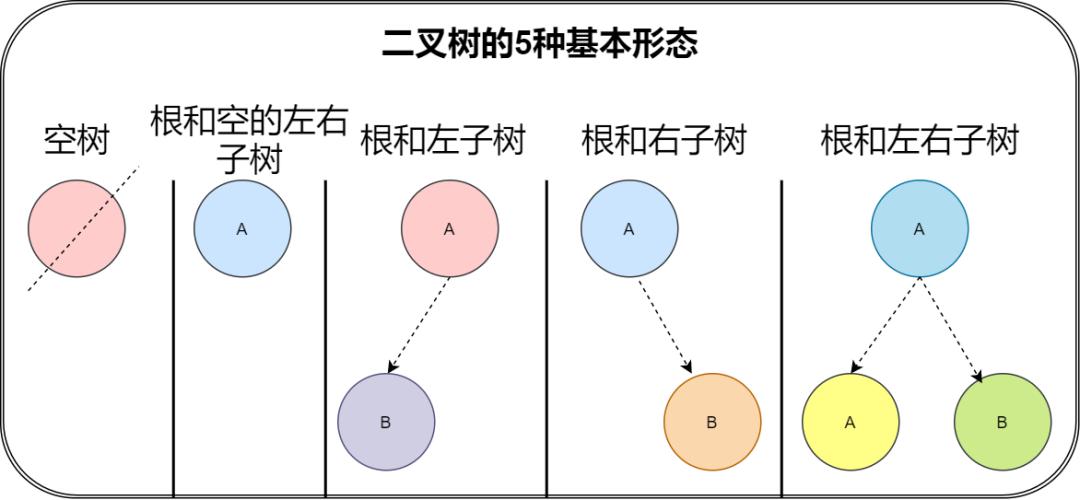
4.2.3 特殊的二叉树
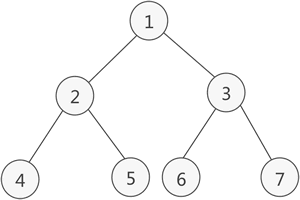
满二叉树:一个二叉树,如果每一个层的结点数都达到最大值,则这个二叉树就是满二叉树。也就是说,如果一个二叉树的层数为K,且结点总数是(2^k) -1 ,则它就是满二叉树。
特点: ①只有最后一层有叶子结点 ②不存在度为1的结点 ③按层序从1开始编号,结点i的左孩子为2i,右孩子为2+1;结点i的父节点为i/2向下取整(如果有的话)
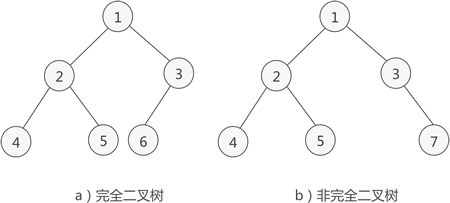
完全二叉树:当且仅当每个结点都与相同高度的满二叉树的编号一一对应
特点: ①只有最后两层可能有叶子结点 ②最多只有一个度为1的结点 ③按层序从1开始编号,结点i的左孩子为2i,右孩子为2+1;结点i的父节点为i/2向下取整(如果有的话) ④i ≤ n/2向下取整为分支结点,i ≥ n/2向下取整为叶子结点
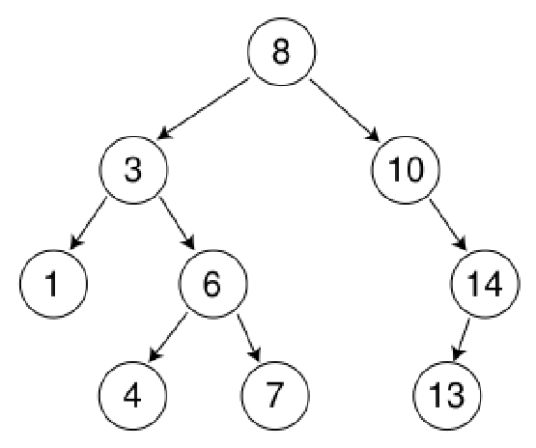
二叉排序树:一棵二叉树或者是空二叉树,或者是具有如下性质的二叉树:左子树上所有结点的关键字均小于根结点的关键字;右子树上的所有结点的关键字均大于根结点的关键字。
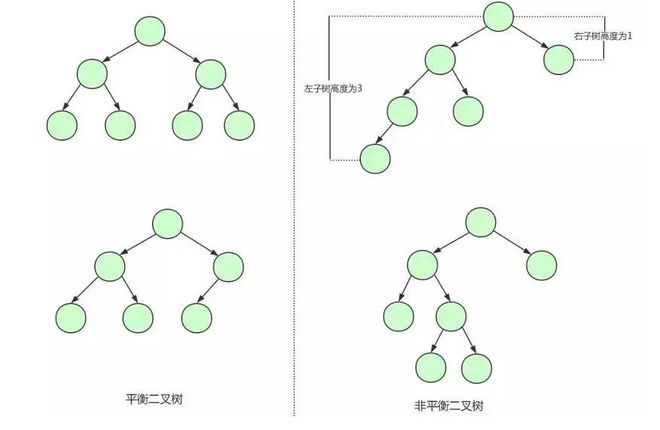
平衡二叉树:树上任一结点的左子树和右子树的深度之差不超过1。
4.2.4 二叉树的性质
几个重要常考的基本操作:
i的左孩子——2i
i的右孩子——2i+1
i的父节点——i/2向下取整
i所在的层次 ——log2(n+1)向上取整 或 log2n向下取整+1
若完全二叉树中共有n个结点(非完全二叉树不行),则
- 判断i是否有左孩子?——2i≤n则有
- ·判断是否有右孩子?——2i+1<n则有
- 判断i是否是叶子/分支结点?——i>n/2向下取整是叶子结点,i<n/2向下取整是分支结点
4.2.5 存储结构
顺序存储和链式存储,一般用链式存储
4.2.6 二叉树的顺序存储
只适合存完全二叉树,普通二叉树会浪费很多空间
二叉树的类型描述
#define MaxSize 10
struct TreeNode{
Elemtype value; //结点中的数据元素
bool isEmpty; //结点是否为空
};
TreeNode t[MaxSize];
初始化
//初始化
bool initBTree(TreeNode &t){
for(int i=0; i<MaxSize; i++){
t[i].isEmpty = true;
}
}
4.2.7 二叉树的链式存储(二叉链表)
二叉树的类型表述
typedef struct TreeNode{
Elemtype data; //数据域
struct BiTNode *lchide, *rchild; //左、右孩子指针
}BiTNode, *BiTree;
注:n个结点的二叉链表共有n+1个空链域
因为n个结点,有n-1个有指向;2n个指针,则指向NULL的个数=2n-(n-1)=n+1
初始化(部分代码)
//数据域
struct Elemtype{
int value;
};
//定义一颗空树
BiTree root = NULL;
//插入根结点
root = (BiTree)malloc(sizeof(BiTNode));
root->data = {1};
root->lchild = NULL;
root->rchild = NULL;
//插入新结点
BiTNode *p = (BiTNode *)malloc(sizeof(BiTNode));
p->data = {2};
p->lchild = NULL;
p->rchild = NULL;
root->lchild = p; //作为根结点的左孩子
找结点p的父节点很难,解决:
typedef struct TreeNode{
Elemtype data; //数据域
struct BiTNode *lchide, *rchild; //左、右孩子指针
struct BiTNode *parent; //父节点指针
}BiTNode, *BiTree;
4.2.8 二叉树的遍历
先序遍历、中序遍历、后序遍历
先序遍历:根左右(NLR)
中序遍历:左根右(LNR)
后序遍历:左右根(LRN)
代码:(用二叉树的链式存储)
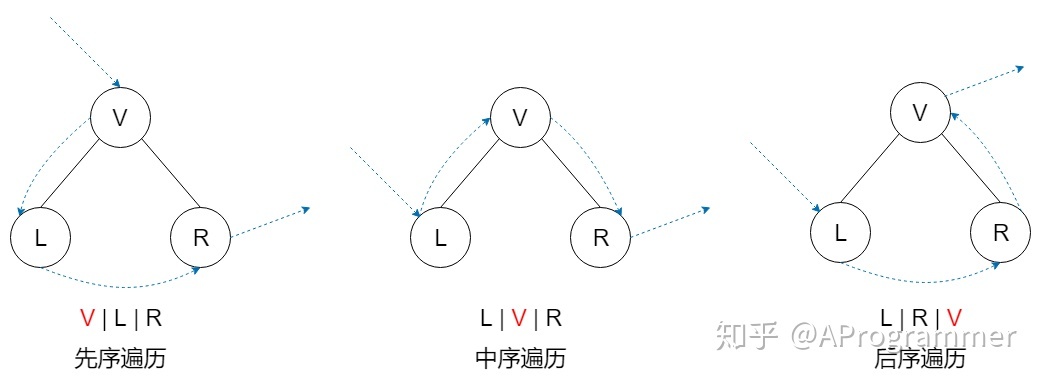
先序遍历:每个结点都会被路过3次,第一次路过时访问结点
空间复杂度=O(h)
//先序遍历
void PreOrder(BiTree T){
if(T!=NULL){
visit(T); //访问根结点
PreOrder(T->lchild); //递归遍历左子树
PreOrder(T->rchild); //递归遍历右子树
}
}
中序遍历:每个结点都会被路过3次,第二次路过时访问结点
空间复杂度=O(h)
//中序遍历
void InOrder(BiTree T){
if(T!=NULL){
InOrder(T->lchild); //递归遍历左子树
visit(T); //访问根结点
InOrder(T->rchild); //递归遍历右子树
}
}
后序遍历:每个结点都会被路过3次,第三次路过时访问结点
空间复杂度=O(h)
//后序遍历
void PostOrder(BiTree T){
if(T!=NULL){
PostOrder(T->lchild); //递归遍历左子树
PostOrder(T->rchild); //递归遍历右子树
visit(T); //访问根结点
}
}
应用:
1.算数表达式的分析树
先序遍历->前缀表达式
中序遍历->中缀表达式(需要加界限符)
后序遍历->后缀表达式
2.求树的深度
//求树的深度
void treeDepth(BiTree T){
if(T!=NULL){
return 0;
}else{
int l = treeDepth(T->lchild); //左子树高度
int r = treeDepth(T->rchild); //右子树高度
//树的深度=Max(左子树深度,右子树深度)+1
return l>r ? l+1 : r+1;
}
}
4.2.9 二叉树的层次遍历(层序遍历)
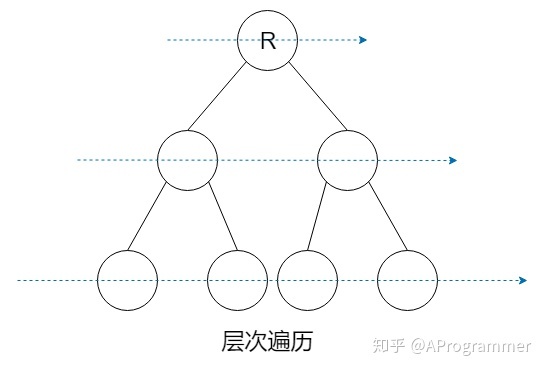
算法思想: ①初始化一个辅助队列(链队列) ②根结点入队 ③若队列非空,则队头结点出队,访问该结点并将其左、右孩子插入队尾(如果有的话) ④重复③直至队列为空
链队列
//类型描述
typedef struct LNode{ //定义单链表结点类型
ElemType data; //数据域,可以是别的各种数据类型,本文统一用int类型
struct LNode *next; //指针域
}LNode;
typedef struct{
LNode *front, *rear;
}LinkQueue;
代码:(用二叉树的链式存储)
//层次遍历
void LevelOrder(BiTree T){
LinkQueue Q;
InitQueue(Q);
BiTree p; //T为根结点,p也是根结点,保证根出队后可以指向孩子,因为T出队后,T->lchild无效
EnQueue(Q, T); //根结点入队
while(!isEmpty(Q)){ //队列不空则循环
DeQueue(Q, T); //根结点出队
if(p->lchild!=NULL)
EnQueue(Q, p->lchild); //左结点入队
if(p->rchild!=NULL)
EnQueue(Q, p->rchild); //右结点入队
}
}
4.2.10 由遍历序列构造二叉树
1.前序+中序遍历序列
2.后序+中序遍历序列
3.层序+中序遍历序列
关键是有非中序确定根结点是谁,再将根结点代入中序得左右子树,依次类推。