4.1 树

4.1.1 树的定义：

树是η(n≥0)个结点的有限集合,n≡o时,称为空树,这是一种特殊情况。在任意一棵非空树中应满足: ①有且仅有一个特定的称为根的结点。 ②当n>1时,其余结点可分为m(m>0)个互不相交的有限集合T1,T2…,Tn,其中每个集合本身又是一棵树,并且称为根结点的子树。

img

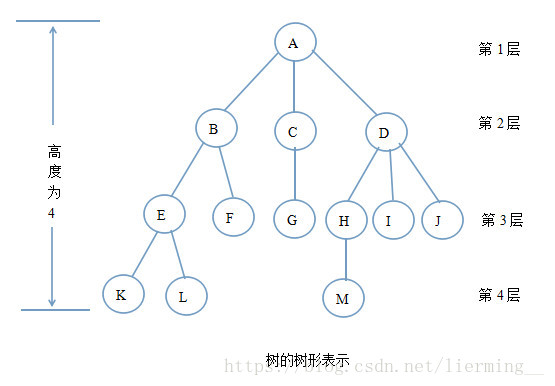
4.1.2 树的术语

父结点：若一个结点含有子结点，则这个结点称为其子结点的父结点 子结点：一个结点含有的子树的根结点称为该结点的子结点 兄弟结点：拥有共同父结点的结点互称为兄弟结点 祖先：对任意结点x，从根结点到结点x的所有结点都是x的祖先（结点x也是自己的祖先） 后代：对任意结点x，从结点x到叶子结点的所有结点都是x的后代（结点x也是自己的后代）

两结点的路径：对任意结点x，从结点x到结点y的从上到下的路 两结点的路径长度：对任意结点x，从结点x到结点y经过的边数

结点的层次：对任意结点x，从根结点到结点x的从上到下经过的边数 结点高度：对任意结点x，叶子结点到x结点的路径长度就是结点x的高度树的深度：一棵树中结点的最大深度就是树的深度，也称为高度

结点的度：有几个子结点（分支） 树的度：各结点的度的最大值 叶子结点：度为零的结点就是叶子结点

森林：m颗互不相交的树构成的集合就是森林

4.2.3 树的分类

有序树和无序树

有序树一一逻辑上看，树中结点的各子树从左至右是有次序的，不能互换

无序树一一逻辑上看，树中结点的各子树从左至右是无次序的，可以互换

4.2.4 树的性质

考点1：结点数=总度数+1

考点2：度为m的树和m叉树 度为m的树：至少有一个结点度=m，一定是非空树 m叉树：允许所有结点的度都≤m，可以是空树

考点3：度为m的树第i层至多有几个结点？ $m^{i-1}$

考点4：高度为h的m叉树至多有几个结点？ $\frac{(m^{h}-1)}{(m-1)}$

考点5： 高度为h的m叉树至少有多少个结点？ $h$

高度为h、度为m的树至少有多少个结点？ $h+m-1$

考点6：具有n个结点的m叉树的最小高度为？ $log_m\lceil (n(m-1)+1) \rceil$