2.9 特殊矩阵的压缩存储

2.9.1 数组的存储结构

一维数组：$a[N]$ 逻辑上连续存放，物理上（内存中）也连续存放 数组元素$a[i]$的物理地址=LOC+i*sizeof(ElemType)

二维数组：$a[N][M]$ 逻辑上是n行n列的矩阵，物理上（内存中）是行优先存储和列优先存储的连续存放 行优先存储：数组元素$a[i][j]$的物理地址=LOC+(i*N+j)*sizeof(ElemType)列优先存储：数组元素$a[i][j]$的物理地址=LOC+(J*M+i)*sizeof(ElemType)

普通矩阵的存储可用二维数组存储。

2.9.2 特殊矩阵的存储

①对称矩阵 ②三角矩阵 ③三对角矩阵 ④稀疏矩阵

对称矩阵的压缩存储

对称矩阵：$a_{i,j}=a_{j,i}$ 方法：一维数组$a[N]$只存主对角线+下三角区（或主对角线+上三角区） 存储数组的大小：$N=\frac{n(n+1)}{2}$ 数组下标范围：$0$ ~ $\frac{n(n+1)}{2}-1$行优先存储：数组下标：$k=\begin{cases} \frac{i(i-1)}{2}+j-1, \quad i \geq j(下三角区和主对角线元素)\\ \frac{j(j-1)}{2}+i-1, \quad i<j(上三角区元素a_{i,j}=a_{j,i}) \end{cases}$

三角矩阵的压缩存储

①下三角矩阵：除主对角线和下三角区，其余的元素都相等 方法：一维数组$a[N]$存主对角线+下三角区，在最后多加一个位置存常其余相等元素 存储数组的大小：$N=\frac{n(n+1)}{2}+1$ 数组下标范围：$0$ ~ $\frac{n(n+1)}{2}$行优先存储：数组下标：$k=\begin{cases} \frac{i(i-1)}{2}+j-1, \quad i \geq j(下三角区和主对角线元素)\\ \frac{n(n+1)}{2}, \quad\quad\quad\quad i<j(上三角区元素) \end{cases}$

②上三角矩阵：除主对角线和上三角区，其余的元素都相等 方法：一维数组$a[N]$存主对角线+下三角区，在最后多加一个位置存常其余相等元素 存储数组的大小：$N=\frac{n(n+1)}{2}+1$ 数组下标范围：$0$ ~ $\frac{n(n+1)}{2}$行优先存储：数组下标：$k=\begin{cases} \frac{(i-1)(2n-i+2)}{2}+(j-i), \quad i \geq j(下三角区和主对角线元素)\\ \frac{n(n+1)}{2}, \quad\quad\quad\quad\quad\quad\quad~ i<j(上三角区元素) \end{cases}$

三对角矩阵的压缩存储

三对角矩阵，又称带状矩阵。 方法：一维数组$a[N]$存带状部分 存储数组的大小：$N=3n-3+1$ 数组下标范围：$0$ ~ $3n-3$行优先存储： i和j计算数组下标k：$k=2i+j-3$数组下标k计算i和j：$i=\lceil (k+2)/3 \rceil$，$j=k-2i+3$

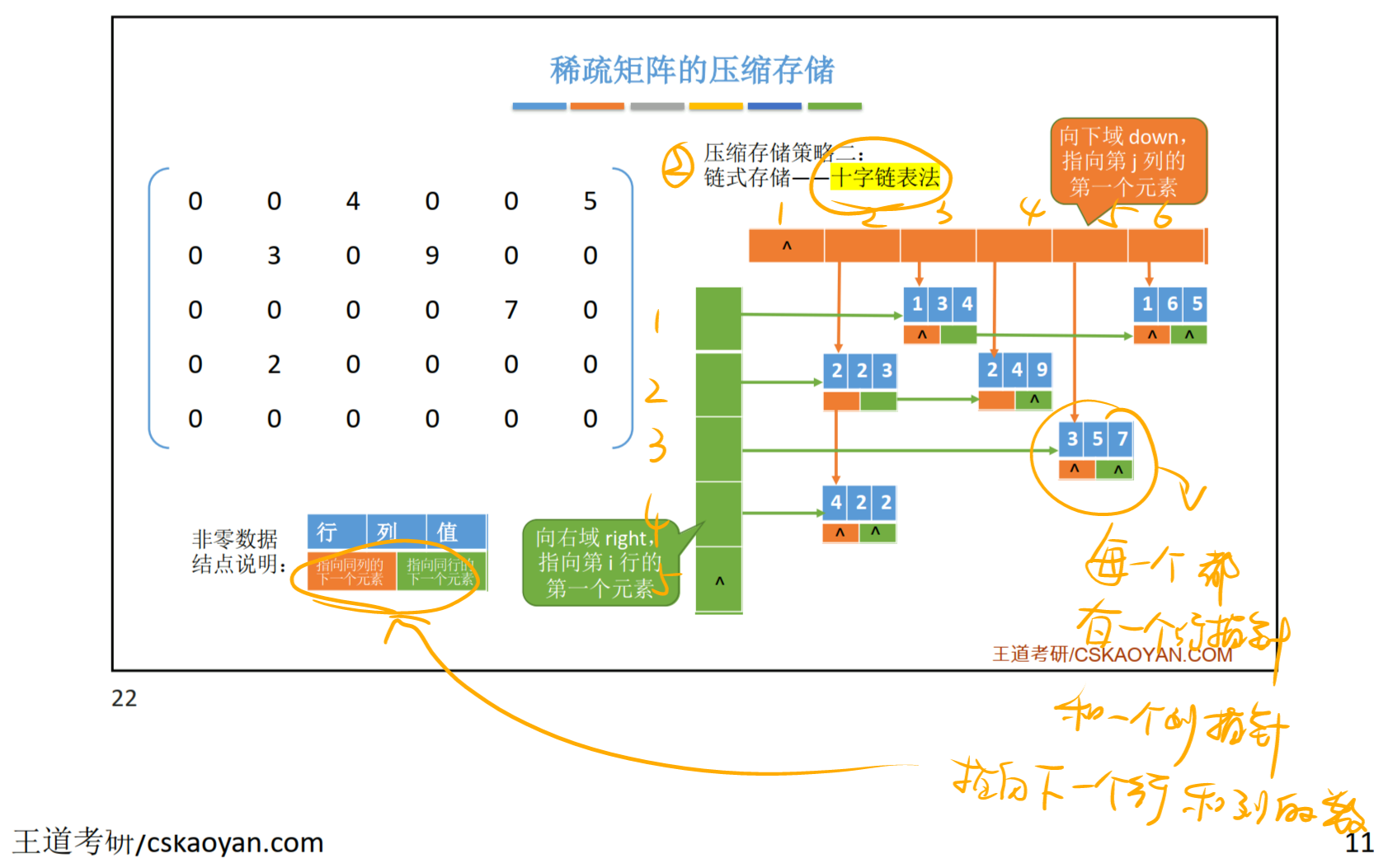
稀疏矩阵的压缩存储

稀疏矩阵：非零元素的个数远远少于矩阵元素的个数。

方法一：顺序存储——三元组<行，列，值>，注：行列从1开始

i（行）	j（列）	v（值）
1	3	4
1	6	5
2	2	3

方法二：链式存储——十字链表法

1637932175187