1.3 线性表的链式存储

1.3.1 单链表的定义

单链表：线性表的链式存储，它是通过一组任意的存储单元来存储线性表中的数据元素，不需要使用地址连续的存储单元，因此它不要求在逻辑上相邻的两个元素在物理位置上也相邻。

1.3.2 单链表的特点

①不能随机访问：遍历查找访问

②存储密度不高：每个节点既要存数据元素又要存指针

③拓展容量方便：直接用建立单链表拓展

④插入、删除操作方便：知道位置直接插入和删除

1.3.3 单链表的实现方式

实现方式：不带头结点和带头结点，一般带头结点比不带头结点好

带头结点：写操作代码方便，一般用带头结点，不明确的都是带头结点的

不带头结点：写操作代码麻烦，要区分第一个数据和后续数据的处理

注：这两种方式主要是：类型描述相同，初始化和判空不同

1.3.4 单链表上的操作

单链表的类型描述

typedef struct LNode{    //定义单链表结点类型
	int data;            //数据域，可以是别的各种数据类型，本文统一用int类型
	struct LNode *next;  //指针域
}LNode, *LinkList;

初始化和判空

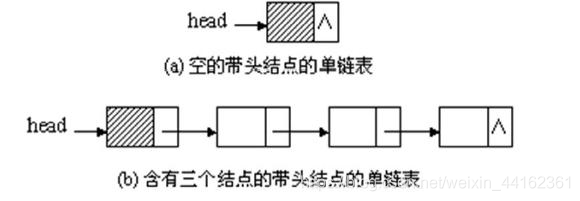
不带头结点的初始化和判空

//初始化
void InitList(LinkList &L){
    L = NULL;
}

//判空操作
bool Empty(LinkList L){
    if(L == NULL){
        return true;
    }else{
        return false;
    }
}

带头结点的初始化和判空

//初始化
void InitList(LinkList &L){
    L = (LNode *)malloc(sizeof(LinkList));
    L->next = NULL;
}

//判空操作
bool Empty(LinkList L){
    if(L->next == NULL){
        return true;
    }else{
        return false;
    }
}

建立单链表

头插法建立单链表

用于链表的逆置

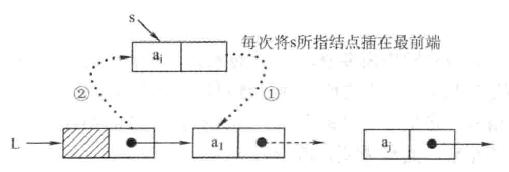
//头插法建立单链表
LinkList HeadInsert(LinkList &L){
    InitList(L); //初始化
    int x;
    cin>>x;/// 相当于scanf
    while(x!=9999){ //输入9999表示结束
        LNode *s = (LNode *)malloc(sizeof(LNode));
        s->data = x;
        s->next = L->next;
        L->next = s;
        cin>>x;/// 相当于scanf
    }
    return L;
}

尾插法建立单链表

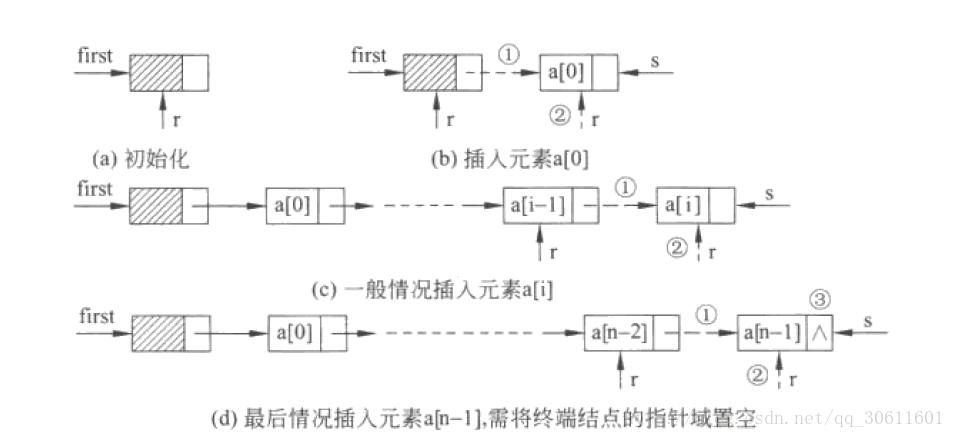
//尾插法建立单链表
LinkList TailInsert(LinkList &L){
    InitList(L);
    LNode *s,*r=L;
    int x;
    cin>>x;/// 相当于scanf
    while(x!=9999){
        s = (LNode *)malloc(sizeof(LNode));
        s->data = x;
        r->next = s;
        r = s;
        cin>>x;/// 相当于scanf
    }
    r->next = NULL;
    return L;
}

插入

时间复杂度=O(1)

带头结点的插入

//将x插入到单链表L的第i个位置上
bool Insert(LinkList &L, int i, int e){
    if(i<1) return false;
    LNode *p = GetElem(L,i-1);    //查找第i个位置
    return InsertNextNode(p, e);  //用后插操作，插在p后面
}

不带头结点的插入

//将x插入到单链表L的第i个位置上
bool Insert(LinkList &L, int i, int e){
    if(i<1) return false;
    if(i==1){
        LNode *s = (LNode *)malloc(sizeof(LNode));
    	s->data = e;
    	s->next = L;
    	L = s;
        return true;
    }
    LNode *p = GetElem(L,i-1);    //查找第i个位置
    return InsertNextNode(p, e);  //用后插操作，插在p后面
}

指定结点的后插操作

//后插操作：在p结点之后插入元素e
bool InsertNextNode(LNode *p, int e){
    if(p==NULL) return false;
    LNode *s = (LNode *)malloc(sizeof(LNode));
	if(s==NULL) return false;
    s->data = e;
    s->next = p->next;
    p->next = s;
    return true;
}

指定结点的前插操作

还是插在p后面，只不过让p和插入结点的值交换

//前插操作：在p结点之前插入元素e
bool InsertPriorNode(LNode *p, int e){
    if(p==NULL) return false;
    LNode *s = (LNode *)malloc(sizeof(LNode));
	if(s==NULL) return false;
    s->next = p->next;
    p->next = s;
    s->data = p->data;
    p->data = e;
    return true;
}

删除

按位序删除

//删除操作:将单链表中的第i个结点删除
bool Delete(LinkList &L, int i, int &e){
    if(i<1 || i>Length(L))
        return false;
    LNode *p = GetElem(L,i-1);  //查找第i-1个位置
    LNode *q = p->next;
    e = q->data;
    p->next = q->next;
    free(q);
    return true;
}

按位序删除的时间复杂度：

最好情况：删除第一个，不需查找位置，循环0次，最好时间复杂度=O(1)

最坏情况：删除最后一个，需查找第n位，循环n次，最坏时间复杂度=O(n)

平均情况：删除任意一个，平均时间复杂度=O(n)

指定结点的删除

时间复杂度=O(n)

方法：p的后一个为q，p指向q的下一个，把q的值给p，最后释放q

//删除指定结点p,采用节点替换法，复制下一个节点的数值，并删除下一个节点
bool Delete(LNode *p){
    if(p==NULL) return false;
    LNode *q = p->next;
    p->data = q->data
    p->next = q->next;
    free(q);
    return true;
}

查找

按位查找

平均时间复杂度=O(n)

//按位查找：查找在单链表L中第i个位置的结点
LNode *GetElem(LinkList L, int i){
    int j=0;
    LNode *p = L;
    if(i<0) return NULL;
    while(p && j<i){
        p = p->next;
        j++;
    }
    return p; //如果i大于表长，p=NULL,直接返回p即可
}

按值查找

平均时间复杂度=O(n)

//按值查找：查找e在L中的位置
LNode *LocateElem(LinkList L, int e){
    LNode *p = L->next;
    while(p && p->data != e){
        p = p->next;
    }
    return p;
}

求表长

平均时间复杂度=O(n)

//求表的长度
int Length(LinkList L){
    int len = 0;
    LNode *p = L;
    while(P->next){
        p = p->next;
        len++;
    }
    return len;
}

遍历

//遍历操作
void PrintList(LinkList L){
    LNode *p = L->next;
    while(p){
        cout<<p->data<<" ";/// 相当于printf
        p = p->next;
    }
    cout<<endl;
}

1.3.5 完整代码

#include<bits/stdc++.h>
using namespace std;

typedef struct LNode{
    int data;
    struct LNode *next;
}LNode, *LinkList;

//初始化
void InitList(LinkList &L){
    L = (LNode *)malloc(sizeof(LinkList));
    L->next = NULL;
}

//遍历操作
void PrintList(LinkList L){
    LNode *p = L->next;
    while(p){
        cout<<p->data<<" ";/// 相当于printf
        p = p->next;
    }
    cout<<endl;
}

//求单链表的长度
int Length(LinkList L){
    LNode *p = L->next;
    int len = 0;
    while(p){
        len++;
        p = p->next;
    }
    return len;
}

//头插法建立单链表
LinkList HeadInsert(LinkList &L){
    InitList(L); //初始化
    int x;
    cin>>x;
    while(x!=9999){
        LNode *s = (LNode *)malloc(sizeof(LNode));
        s->data = x;
        s->next = L->next;
        L->next = s;
        cin>>x;
    }
    return L;
}

//尾插法建立单链表
LinkList TailInsert(LinkList &L){
    InitList(L);
    LNode *s,*r=L;
    int x;
    cin>>x;
    while(x!=9999){
        s = (LNode *)malloc(sizeof(LNode));
        s->data = x;
        r->next = s;
        r = s;
        cin>>x;
    }
    r->next = NULL;
    return L;
}

//按值查找：查找x在L中的位置
LNode *LocateElem(LinkList L, int x){
    LNode *p = L->next;
    while(p && p->data != x){
        p = p->next;
    }
    return p;
}

//按位查找：查找在单链表L中第i个位置的结点
LNode *GetElem(LinkList L, int i){
    int j=1;
    LNode *p = L->next;
    if(i==0)return L;
    if(i<1)return NULL;
    while(p && j<i){
        p = p->next;
        j++;
    }
    return p; //如果i大于表长，p=NULL,直接返回p即可
}

//将x插入到单链表L的第i个位置上
void Insert(LinkList &L, int i, int x){
    LNode *p = GetElem(L,i-1);
    LNode *s = (LNode *)malloc(sizeof(LNode));
    s->data = x;
    s->next = p->next;
    p->next = s;
}

//删除操作:将单链表中的第i个结点删除
void Delete(LinkList &L, int i){
    if(i<1 || i>Length(L)){
        cout<<"delete failed: index is wrong."<<endl;
        return;
    }
    LNode *p = GetElem(L,i-1);
    LNode *q = p->next;
    p->next = q->next;
    free(q);
}


int main(){
    //初始化，尾插法建立单链表
    LinkList L = TailInsert(L);
    //插入：在第二个位置插入结点，数据域为888，并遍历单链表
    Insert(L,2,888);
    cout<<"在第二个位置插入888： ";
    PrintList(L);
    //删除：删除第四个结点
    Delete(L,4);
    cout<<"删除第四个结点后：";
    PrintList(L);
    //按位查找：查找第三个结点，并输出其数据域的值
    LNode *p = GetElem(L,3);
    cout<<"第三个结点的值为："<<p->data<<endl;
    //按值查找：查找数据域为2的结点的指针
    LNode *q = LocateElem(L,2);
    cout<<"数据为2的结点的下一个结点的值为："<<q->next->data<<endl;
    //输出单链表的长度
    cout<<"单链表的长度："<<Length(L)<<endl;
    return 0;
}

运行结果：