3.3 字符串模式匹配

字符串模式匹配：在主串中找到与模式串相同的子串,并返回其所在位置。

子串：一定能在主串中找到的串

模式串：不一定能在主串中找到的串

方法：朴素模式匹配算法和KMP算法

3.3.1 朴素模式匹配算法

用串的定位操作：

方法：在S中依次按顺序取m长子串，判断是否与T相同

//定位操作
int Index(SString S,SString T){
    int i = 1, n = StrLength(S), m = StrLength(T);
    SString sub;
    while(i < n-m+1){
        SubString(sub, S, i, m);
        if(StrCompare(sub, T) != 0) ++i;
        else return i; //返回子串在主串中的位置
    }
    return 0;          //S中不存在与T相同的子串
}

双指针算法

int Index(SString S, SString T){
    int i = 1, j = 1;
    while(i<=S.length && j<=T.length){  //跳出循环情况：j>T.length,匹配成功
        if(S.ch[i]==T.ch[i]){			             //i>S.length,匹配失败
            ++i; ++j;          //继续比较后面的字符
        }else{				   //匹配失败，指针i、j都后退，匹配下一个
            i = i-j+2;
            j = 1;             
        }
    }
    if(j > T.length){          //j>T.length,匹配成功
        return i-T.length;
    }else{
        return 0;
    }
}

朴素模式匹配算法的时间复杂度：

设主串长度为n，模式串长度为m，则

最好情况：每次匹配第一个字符就匹配失败，直到最后才匹配成功，循环n次，最好时间复杂度=O(n)

最坏情况：到最后也没找到，主串移动n个元素，模式串移动m个元素，最坏时间复杂度=O(mn)

3.3.2 KMP算法

精髓：利用好已经匹配过的模式串信息，建立一个next数组，表示j的回溯

int Index(SString S, SString T){
    int i = 1, j = 1;
    while(i<=S.length && j<=T.length){  //跳出循环情况：j>T.length,匹配成功
        if(S.ch[i]==T.ch[i]){			             //i>S.length,匹配失败
            ++i; ++j;          //继续比较后面的字符
        }else{				   //匹配失败，指针i不变，j后退，匹配下一个
            j=next[j];            
        }
    }
    if(j > T.length){          //j>T.length,匹配成功
        return i-T.length;
    }else{
        return 0;
    }
}

KMP算法的时间复杂度：

设主串长度为n，模式串长度为m，则

最好情况：每次匹配第一个字符就匹配失败，直到最后才匹配成功，循环n次，最好时间复杂度=O(n)

最坏情况：到最后也没找到，主串移动n个元素，模式串移动m个元素，最坏时间复杂度=O(m+n)

next数组的建立

P[0 ~ k-1] == P[j-k ~ j-1]

img

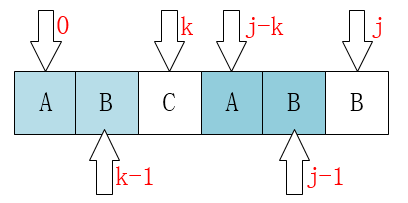
//next数组的建立
int[] getNext(String ps){
    char[] p = ps.toCharArray();
    int[] next = new int[p.length];
    next[1] = 0;
    int j = 1, k = 0;
    while (j < p.length){
    	if (k == 0 || p[j] == p[k]) {
            next[++j] = ++k;
        }else{
            k = next[k];
    	}
    }

    return next;
}